数论2
排列组合
- 加法原理:p1+p2+p3+..+pn;
- 乘法原理:p1xp2xp3x..xpn;
- 容斥原理:|AUBUC|=|A|+|B|+|C|-|AnB|-|BnC|-|AnC|+|AnBnC|;
杨辉三角

根据杨辉三角我们可以与二项式定理进行比较得出一个有趣的结论:(a+b)^n的展开项系数和杨辉三角的行数系数相对应,因此当已知n要求展开项的时候我们可以采取递推或者直接推算的方法。其中前一个是o(n^2)后一个是o(n)。
void calc1()
{
memset(c,0,sizeof(c));
for(int i=0;i<=n;i++)
{
c[i][0]=1;
for(int j=0;j<=i;j++)
c[i][j]=c[i][j-1]+c[i-1][j-1];
}
}void calc2()
{
f[0]=1;
for(int i=1;i<=n;i++)
f[i]=f[i-1]*(n-i+1)/i;
}约数个数
求正整数n的正约数的个数:
首先直接进行求唯一分解式:n=p1^a1xp2^a2xp3^a3xpn^an,接下来就可以直接推出答案ans=(a1+1)x(a2+1)x…x(an+1)
欧拉函数
求与正整数n互素的数的个数:
假设一个正整数n与正整数k不互素,同时n>k,那么k的x倍(xk<n)都与n不互素,因此只要减去与之不互素的数和它的倍数即可,可以推出公式:φ(n)=n(1-1/p1)(1-1/p2)…(1-1/pk)
int phi(int n)
{
int ans=n,m=(int)sqrt(n+0.5);
for(int i=2;i<=m;i++)
if(n%i==0){
ans=ans*(i-1)/i;
while(n%i==0) n/=i;
}
if(n>1) ans=ans*(n-1)/n;
return ans;
}欧拉函数的线性筛,时间复杂度是O(nloglogn):
void f(int n)
{
for(int i=2;i<=n;i++) phi[i]=0;
phi[1]=1;
for(int i=2;i<=n;i++)
if(!phi[i])
for(int j=i;j<=n;j+=i){
if(!phi[j]) phi[j]=j;
phi[j]=phi[j]*(i-1)/i;
}
}编解码
之前提到的字典序的全排列问题,我们用while(next_permutation)去打印所有的全排列,但是引出了一个问题,我们可否根据一个任意的字符串来求出他是第几个全排列,或者反之直接求出第n个序列,这时候就可以用上我们的编解码了。
假设一个字符串由aabc组成,我们讨论它编码的问题,设d(s)代表小于s的串的个数,f(s)代表s的全排列数量,比如现在求caba在aabc全排列的位置,我们就可以通过下面的图来解释,那么f(s)怎么求,我们用组合数学的公式,设字符共有k类,个数分别是n1,n2…nk个,那么f(s)=(n1+n2+…+nk)!/n1!n2!…nk!。同样的解码问题可以引申为下图的右侧。
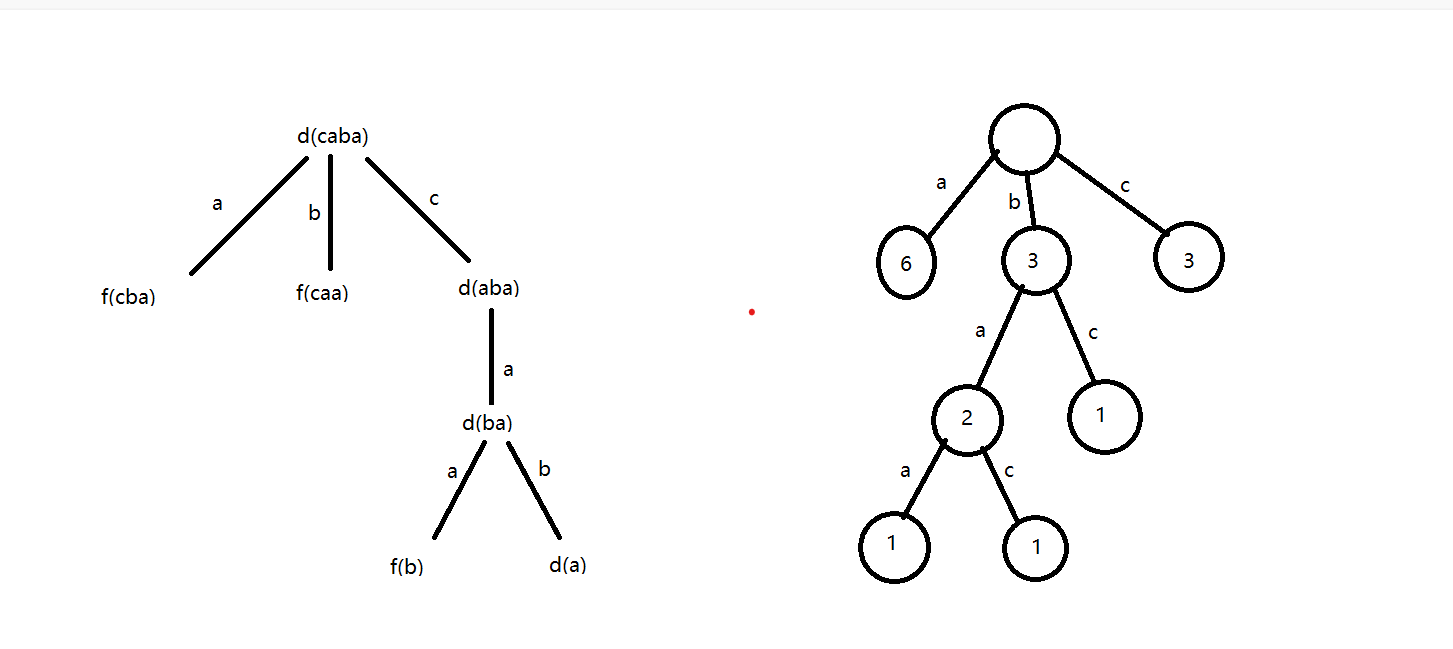
离散概率
这真算是离散数学的开端了,就直接介绍几个简单的概率问题:
样本空间
设所有会发生的事情是样本空间|S|然后会发生的事件为|E|,直接求出答案:P(E)=|E|/|S|。
补集概念
有时候正向求概率的时候不容易推导,我们用求1-k的方式去求解,但是在算的时候要注意double的范围问题,推荐用边乘边除的方式:
P(E)=1-P(/E)=1-P(E1)P(E2)P(E3)……P(En)=1-n/nx(n-1)/nx(n-2)/n……(n-(m-1))/n。
条件概率
B事件发生的情况下A的概率:P(A|B)=P(AB)/P(B)
全概率公式
P(A)=P(A|B1)xP(B1)+P(A|B2)xP(B2)+…+P(A|Bn)xP(Bn)
贝叶斯公式
P(A|B)=P(A)/(P(A|B1)xP(B1)+P(A|B2)xP(B2)+…+P(A|Bn)xP(Bn))
